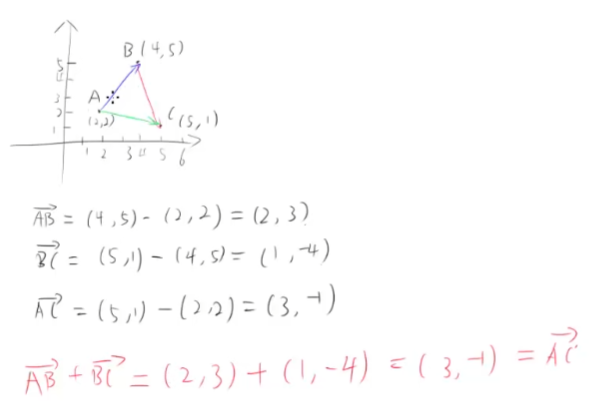算错了 -35
Unity - A计划（永久有效期）
![]()
扫二维码继续学习 二维码时效为半小时
18
渲染流水线三大阶段：
1.应用阶段：Cpu负责（绝对控制权）（1）准备场景数据（2）.不可见剔除（3）.设置渲染状态
分三步：1.把数据加载到显存中。2.设置渲染状态3.调用Draw Call。
2.几何阶段:
GPU负责。首要任务是把顶点坐标变换到屏幕空间中，再交给光栅器进行处理。
3.光栅化阶段：GPU负责。使用上个阶段传递的数据来产生屏幕上像素并最终渲染出图像
1.opengl es针对yi'dong'duan
在推导
你是谁
漫反射
（本节介绍了，漫反射与点乘的关系，有必要学一下）
（讲解为什么法线向量与入射光线的点乘为COS角度）
当光线垂直射入物体后，反射的光线是最强的。
当光线几乎平行于表面，反射的光线是最弱的。
C (diffuse) = C (光) . m (物体) . max(0,（n向量 . l 向量）)
自发光与环境光
（本节介绍 自发光 和 环境光 的概念，没必要听）
光照的介绍
（本节就是了解概念）
反色率 = 入射角 / 折射角
BRDF ： 光照模型
（次世代渲染技术）
sss材质 ： 次表面散射
Shader Target
unity 支持的Shader Target
#pragma target 2.0 - 5.0
Shader Model 1 、2、3、.... 可以理解为是C#语言的不同版本。
矩阵的简单介绍
矩阵分 行 和 列
例如：
3 X 4 阶矩阵
3 是 行
4 是 列
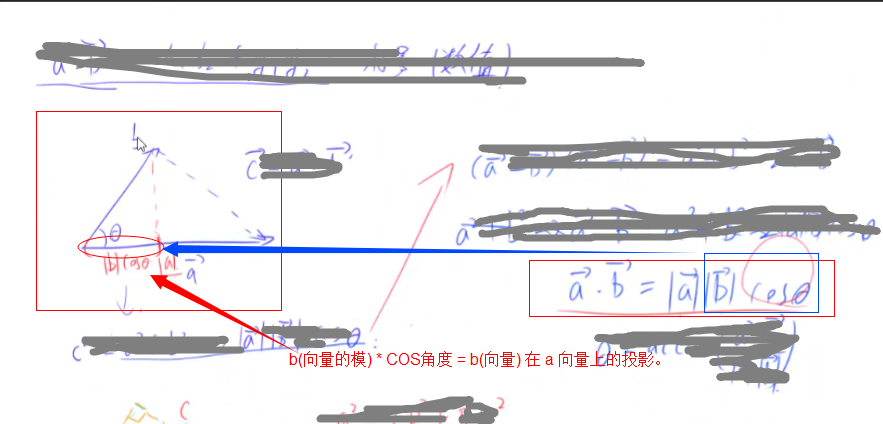
向量点乘
向量点乘的几何意义
a(向量） * b(向量) > 0
向量夹角 < 90° cos 为 正 [ -90 , 90 ]
a(向量） * b(向量) = 0
向量垂直 cos 为 0 （ -90 , 90 ，270 ，... )
a(向量） * b(向量) < 0
向量夹角 > 90° cos 为 负 [ -90 , -270 ]
向量的点乘 有 2 个公式
（ 这2个公式求得的最后结果都是一样的，一个标量 ）
公式1：
OA(向量) * OB(向量) = ( x1 * x2 ) + ( y1 * y2 )
公式2：
OA(向量) * OB(向量) = OA(向量的模) * OB(向量的模) * COS（向量夹角）
（1、灵活运用这2个公式可以求的俩个向量的点乘
2、也可以求的俩个向量的夹角
3、一个向量在另一个向量上的投影。）
俩个向量之间的点乘相当于，A 向量在 B 向量上的投影 * B 向量的模长
三维向量叉乘
I a(向量) x b(向量) I = I a(向量) I I b(向量) I sin角度
叉乘得到的最终向量的方面，按照所遵循的左手和右手定则 而不同。
叉乘的意义：
判断三角面的朝向。
叉乘的值
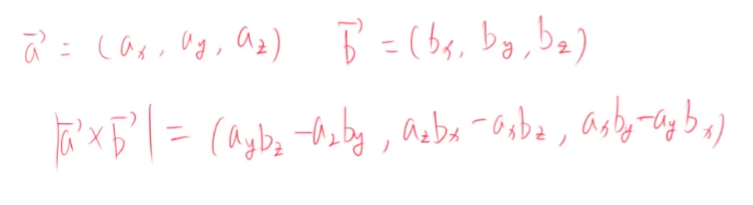
三维向量基本运算
三维坐标系中的向量OP
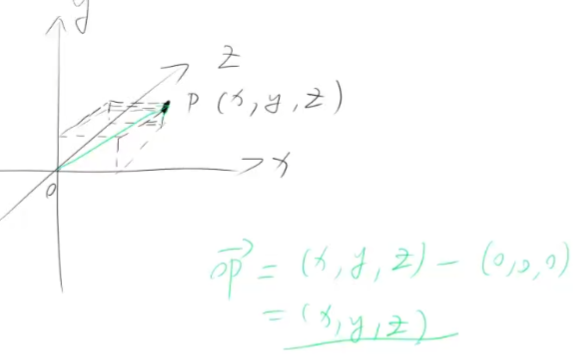
三维向量的加减法 和 模 的计算， 和二维向量基本一致，只是多了一个Z轴需要参与运算
加减法
模的计算
[ x(平方) +y(平方) +z(平方) ](开根号)
三维坐标系
三维坐标系，分为左右手坐标系。
就像OpenGL 和 DX 一样。
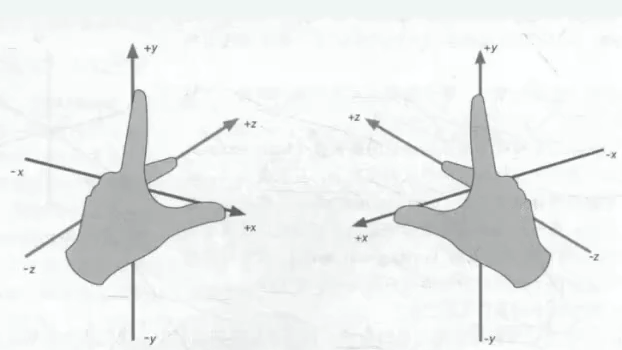
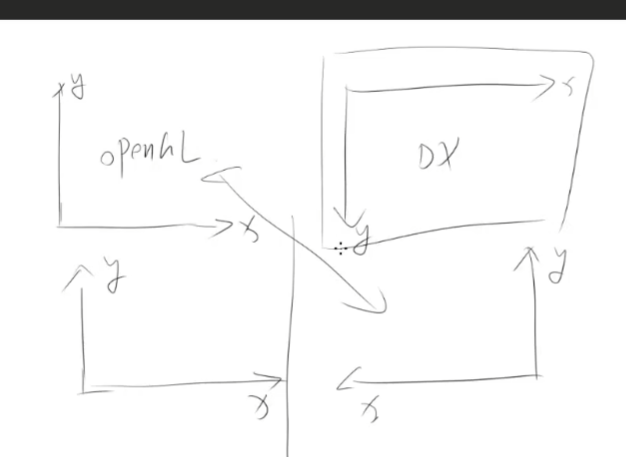
OpenGL 先旋转180度 在镜像 得 DX
Unity 是左手坐标系
二维坐标系旋转和平移
x = x` cos角度 + y`sin角度 + a
y = y` cos角度 - x`sin角度 + b
(a,b) 是坐标平移的向量
角度 是坐标先转的角度。
二维向量的叉乘
叉乘的其他叫法：
向量积，外积，叉积
点乘最后生成的是一个标量。
叉乘最后生成的是一个向量。
叉乘
a (向量) * b（向量）= c（向量）
（叉乘后得到的最终向量）
模长：
|c| = | a(向量) * b（向量）| =|a| |b| sin角度
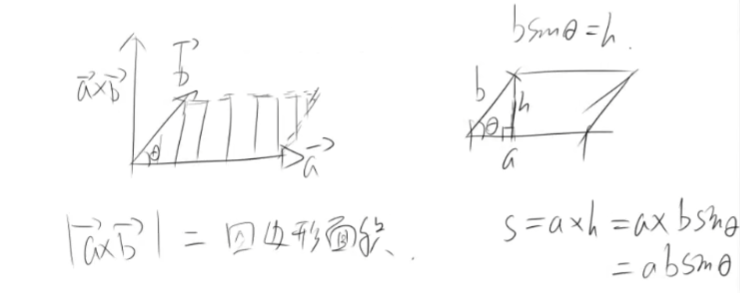
方向：
c(向量) 的方向垂直于 a(向量) 与 b（向量）所在平面。
二维向量的点乘
1、a(向量) 点乘 b(向量) = x1x2 + y1y2 = 标量（数值）
=a(向量的模长) * b(向量的模长) cos(角度)
向量的点乘 可以换算成角度
角度 = ac cos( (a(向量) * b(向量) ) / a(向量模长) * b(向量模长) )
2、余弦定理
余弦定理推演：
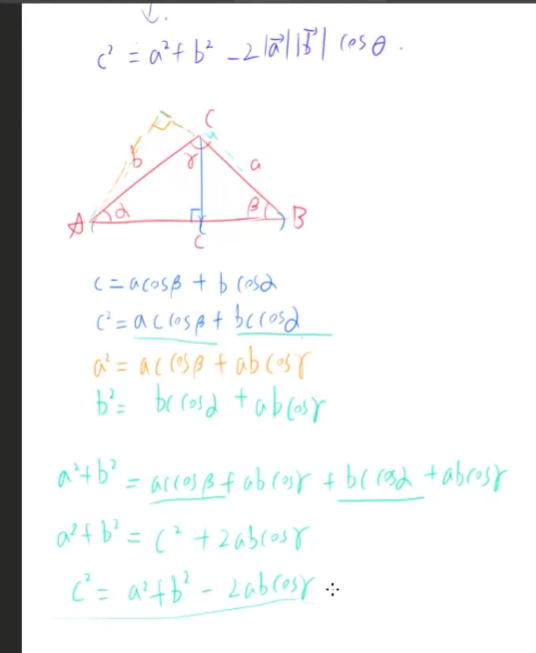
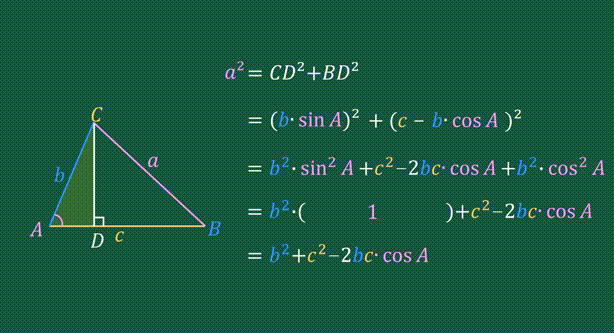
余弦定理的推理是通过，三角函数平方关系+勾股定理 一起推演出来的。
三角函数平方关系：
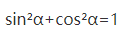
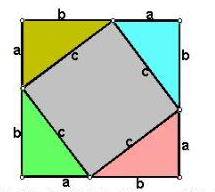
勾股定理：
直角三角形 俩个直角边的平方和等于对边的平方
二维向量减法
二维向量的加法 = a(向量) + b(向量)
二维向量的减法 = a(向量) + -b(向量)
二维向量减法： 被减向量 与 减向量 平移到共起点， 减法得到的最终二维向量是 减向量的终点为起点，指向被减向量的终点。
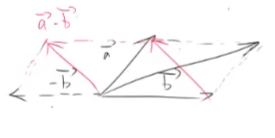
二维向量加法
