代数余子式性质
--------------------------
证明:D = a_(ij)A_(ij)
如果a_(ij) 在第一行第一列
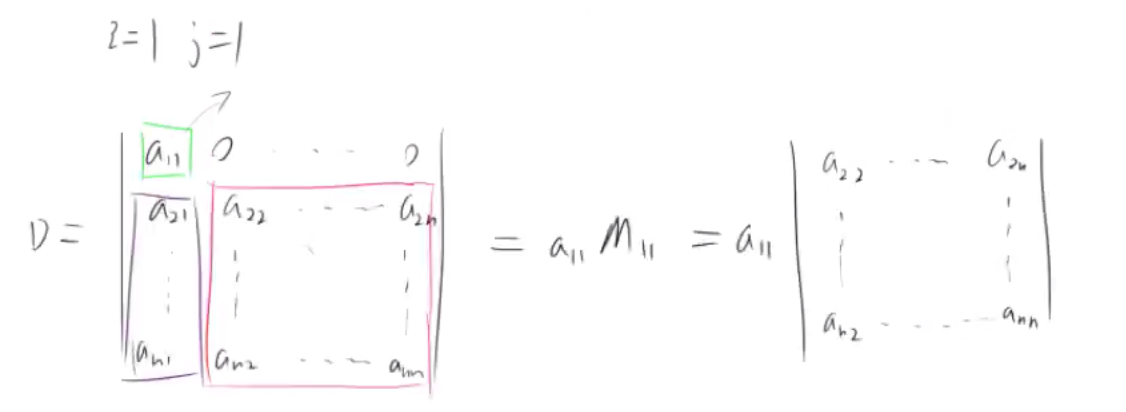
===================
如果a_(ij) 不在第一行第一列
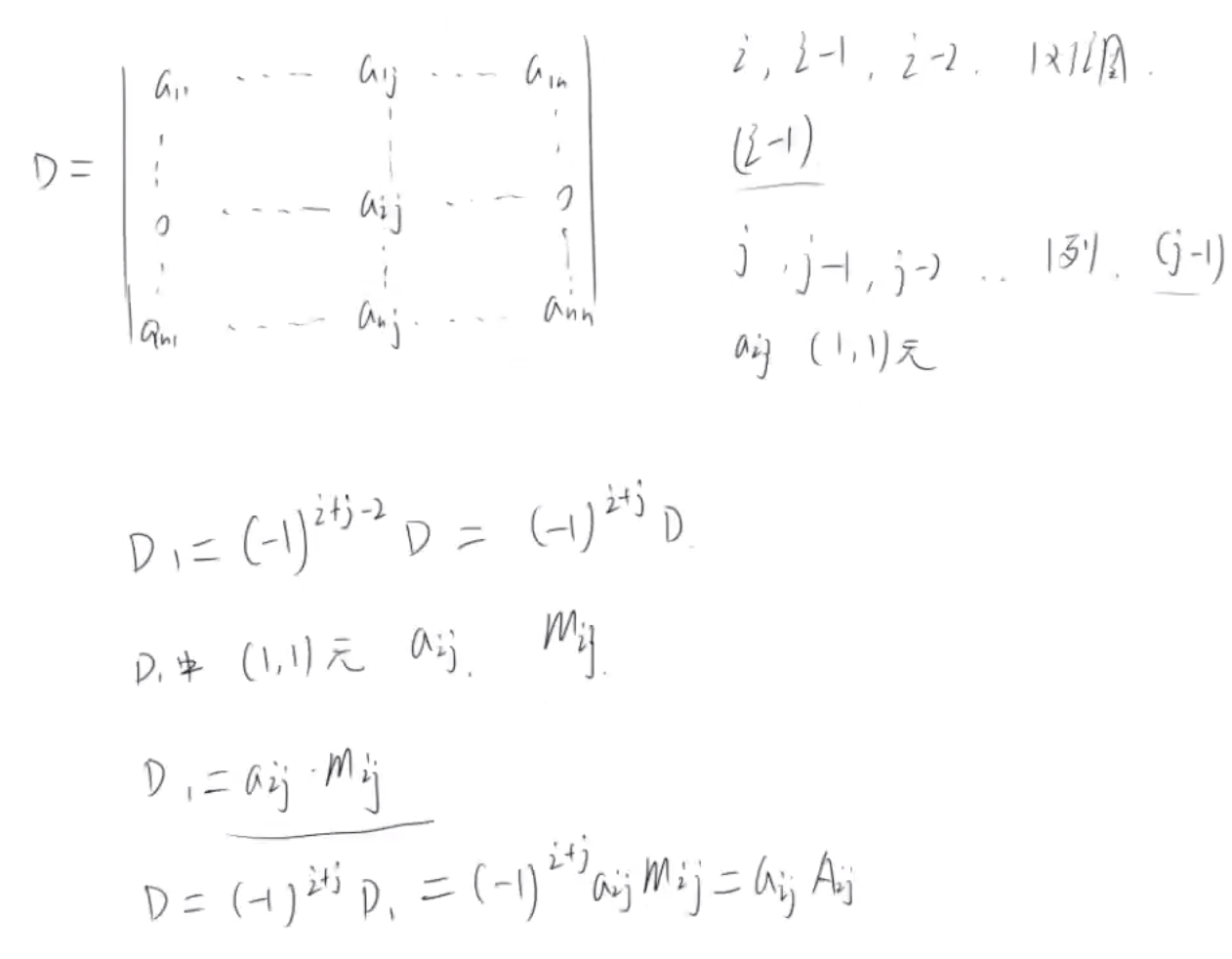
代数余子式性质
--------------------------
证明:D = a_(ij)A_(ij)
如果a_(ij) 在第一行第一列

===================
如果a_(ij) 不在第一行第一列
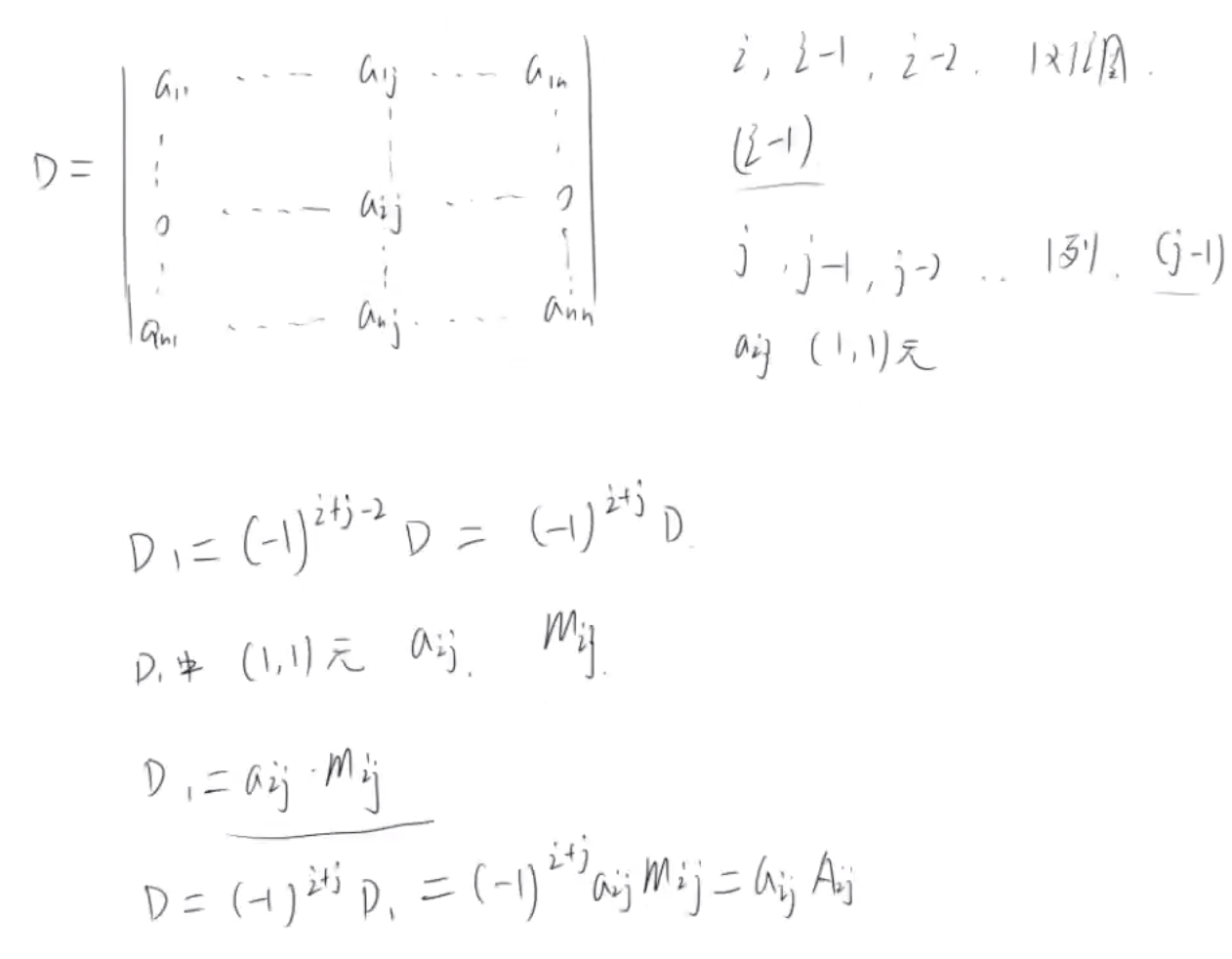
行列式证明三角行列式性质
--------------------------
如果已知

那么 D = D_1D_2
==================
一个n阶行列式,如果其中第i行所有元素除(i,j)元 a_(ij) 外都为0,那么这个行列式就等于:
D = a_(ij)A_(ij)
行列式性质补充
--------------------------
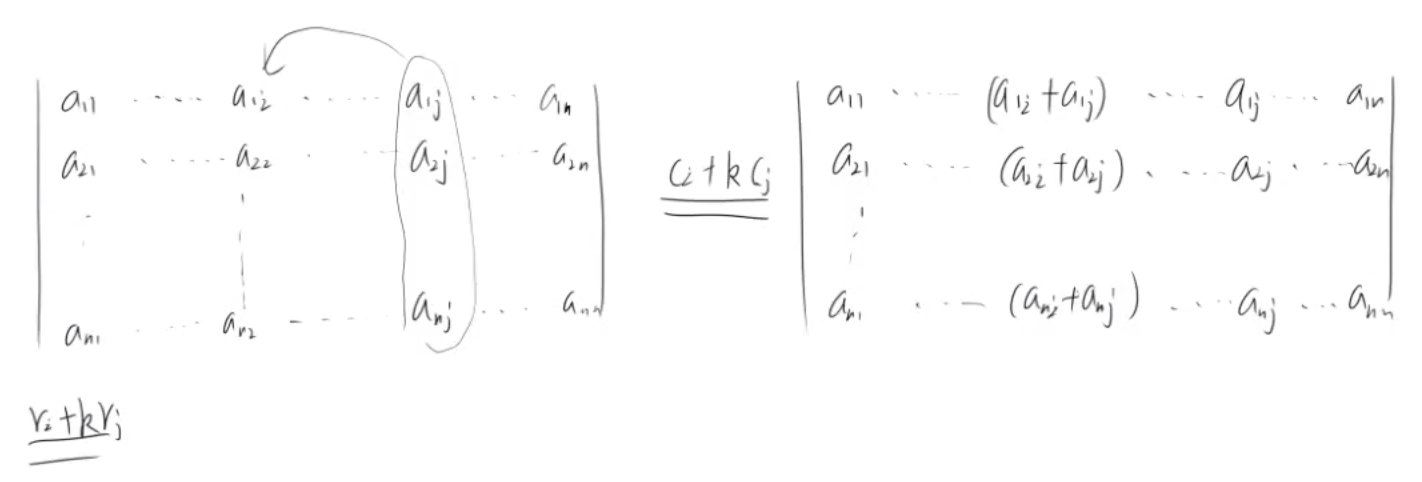
把行列式某一行(列)的各元素乘以同一数后加到另一行(列)对应元素上,行列不变
三角行列式

行列式性质
--------------------------
余子式
| 3 4 5 |
M = | 6 7 8 |
| 2 3 4 |
| 6 8 |
M^(12) = | 2 4 |
M^(12) 叫做M当余子式
note: 在M的基础上,去除第1行,去除第2列 所得到第新的矩阵
===================
矩阵的代数余子式
C_(ij) = (-1)^(i+j) | M^(ij) |;
===================
行列式的性质
1. 行列式与它的转制的值相等 D^T = D
2. 互换行列式两行(列),行列式变号
3. 行列式某一行(列)中所有元素都乘以同一数k,等于用k乘此行列式
4. 如果行列式中如果有两行(列)元素成比例,行列式D = 0
5. 若行列式中某一行(列)的元素都是两数之和,可以把行列式分开写
e.g. (行列式D 某一列 满足条件)
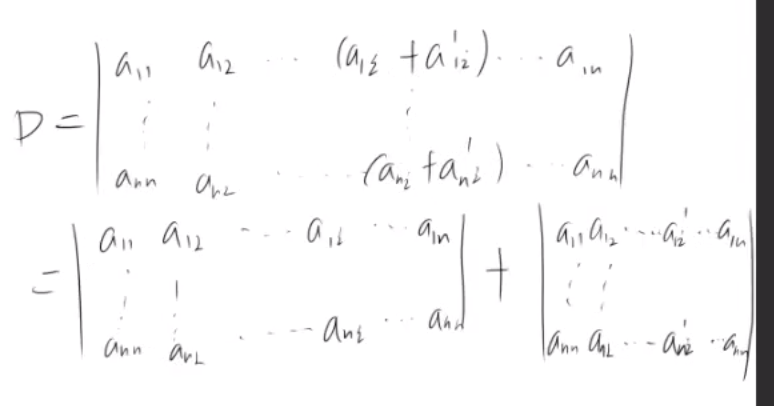
6. 把行列式某一行(列)的各元素乘以同一数后加到另一行(列)对应元素上,行列不变
三阶行列式
--------------------------
| m_11 m_12 m_13 |
M = | m_21 m_22 m_23 |
| m_31 m_32 m_33 |
| M | = m_11m_22m33 +m_12m_23m_32 + m_13m_21m_32 - m_13m_22m_31 - m_32m_23m_11 - m_21m_12m_33 ;
==============
三维叉乘
Vector3D a,b;
i = (1,0,0)
j = (0,1,0)
k = (0,0,1)
| i j k |
a x b = | a.x a.y a.z | = (a.y b.z - b.y a.z)i - (a.x b.z - b.x a.z)j + (a.x b.y - b.x a.y)k ;
| b.x b.y b.z |
a x b = (a.y b.z - b.y a.z)i - (a.x b.z - b.x a.z)j + (a.x b.y - b.x a.y)k ;
二阶行列式
--------------------------
| m_11 m_12 |
M = | m_21 m_22 |
| M | = m_11m_22 - m_12m_21
=====================
extra note:
行列式与矩阵的区别与联系
1、行列式的本质是线性变换的放大率,而矩阵的本质就是个数表。
2、行列式行数=列数,矩阵不一定(行数列数都等于n的叫n阶方阵),二者的表示方式亦有区别。
3、行列式与矩阵的运算明显不同
1) 相等:只有两个同型的矩阵才有可能相等,并且要求对应元素都相等;而两个行列式相等不要求其对应元素都相等,甚至阶数还可以不一样,只要两个行列式作为两个数的值是相等即可。
2) 加(减)法:两个矩阵相加(减)是将其对应元素相加(减),因此只有同型的矩阵才可以相加(减);而两行列式作为两个数总是可以相加(减)的。
3) 数乘运算:一个数乘以矩阵是指该数乘以矩阵的每一个元素;而数乘行列式,只能用此数乘行列式的某一行或列,提取公因数也是如此。
4) 乘法:矩阵的乘法不满足交换律,所以,一般地, AB≠BA。但是,如果 A与 B 都是 n 阶方阵,则有 |AB|=|A| |B|=|B| |A|=|BA|。
Reference:
百度知道, 2018, 行列式与矩阵的区别与联系, Link: https://zhidao.baidu.com/question/97241681.html [Accessed Date: 2018/04/12]
切变
--------------------------
面积,体积无变化
x' = x + sy
s 为因子
=================
2D切变矩阵
┌ 1 0 ┐
H_x(s) = └ s 1 ┘
┌ 1 s ┐
H_y(s) = └ 0 1 ┘
==================
3D切变矩阵
┌ 1 0 0 ┐
H_(xy)(s,t) = │ 0 1 0 │
└ s t 1 ┘
┌ 1 0 0 ┐
H_(xz)(s,t) = │ s 1 t │
└ 0 0 1 ┘
┌ 1 s t ┐
H_(yz)(s,t) = │ 0 1 0 │
└ 0 0 1 ┘
镜像矩阵
--------------------------
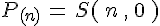
0 为缩放因子,
当缩放因子为0,代表了投影
当缩放因子为-1,代表了镜像
======================
e.g. 二维 运算法则 当缩放因子为 -1
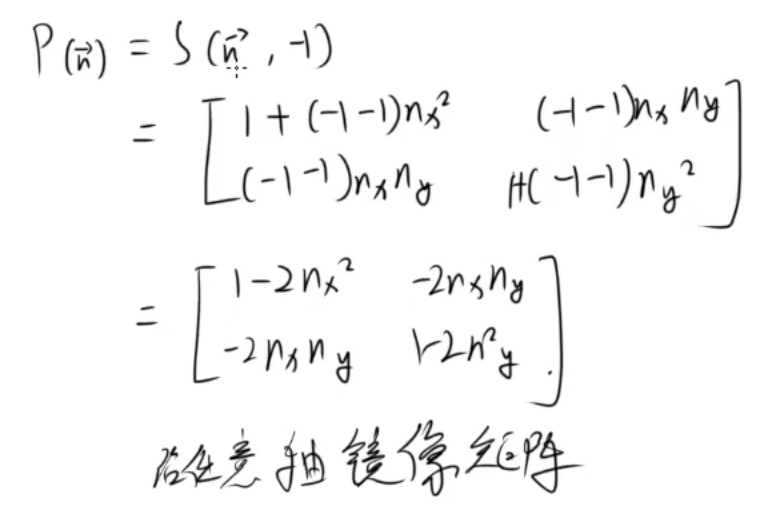
======================
三维
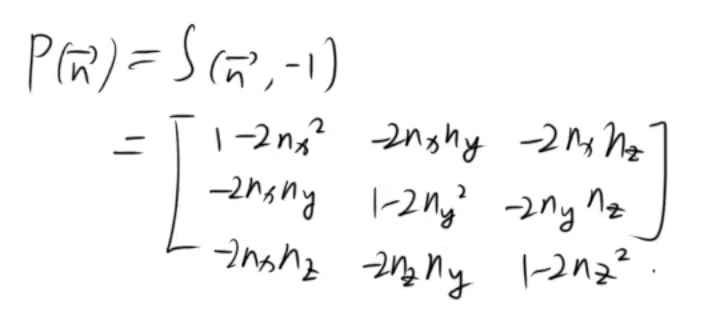
正交投影矩阵
--------------------------

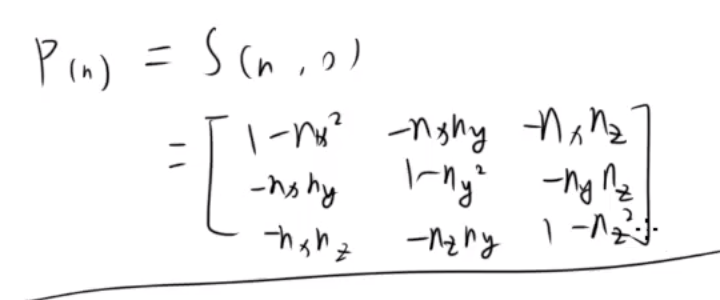
正交投影
--------------------------
二维
向X轴投影
┌ 1 0 ┐
p_x = └ 0 0 ┘
向Y轴投影
┌ 0 0 ┐
p_y = └ 0 1 ┘
================
三维
向xy平面投影
┌ 1 0 0 ┐
p_xy = │ 0 1 0 │
└ 0 0 0 ┘
向xz平面投影
┌ 1 0 0 ┐
p_xz = │ 0 0 0 │
└ 0 0 1 ┘
向yz平面投影
┌ 0 0 0 ┐
p_yz = │ 0 1 0 │
└ 0 0 1 ┘
沿任意方向三维缩放矩阵
--------------------------
Vector p, q, r;
p = [1,0,0];
┌ 1 + (k-1)(n_x)^2 ┐
p' = │ (k-1)n_xn_y │
└ (k-1)n_xn_z ┘
q = [0,1,0];
┌ (k-1)n_xn_y ┐
q' = │ 1 + (k-1)(n_y)^2 │
└ (k-1)n_yn_z ┘
r = [0,0,1];
┌ (k-1)n_xn_z ┐
r' = │ (k-1)n_zn_y │
└ 1 + (k-1)(n_z)^2 ┘
┌ p' ┐ ┌ 1 + (k-1)(n_x)^2 (k-1)n_xn_y (k-1)n_xn_z ┐
S(n,k) = │ q' │ = │ (k-1)n_xn_y 1 + (k-1)(n_y)^2 (k-1)n_yn_z │
└ r' ┘ └ (k-1)n_xn_z (k-1)n_zn_y 1 + (k-1)(n_z)^2 ┘
沿任意方向缩放二维矩阵
--------------------------
Vector2D p, q;
缩放系数k,缩放轴n;
矩阵推导
p = [1,0];
q = [0,1];
┌ 1 + (k-1)(n_x)^2 ┐
p' = └ (k-1)n_xn_y ┘
┌ (k-1)n_xn_y ┐
q' = └ 1 + (k-1)(n_y)^2 ┘
┌ p' ┐ ┌ 1 + (k-1)(n_x)^2 (k-1)n_xn_y ┐
S(n,k) = └ q' ┘ = └ (k-1)n_xn_y 1 + (k-1)(n_y)^2 ┘
沿任意方向缩放推演
--------------------------
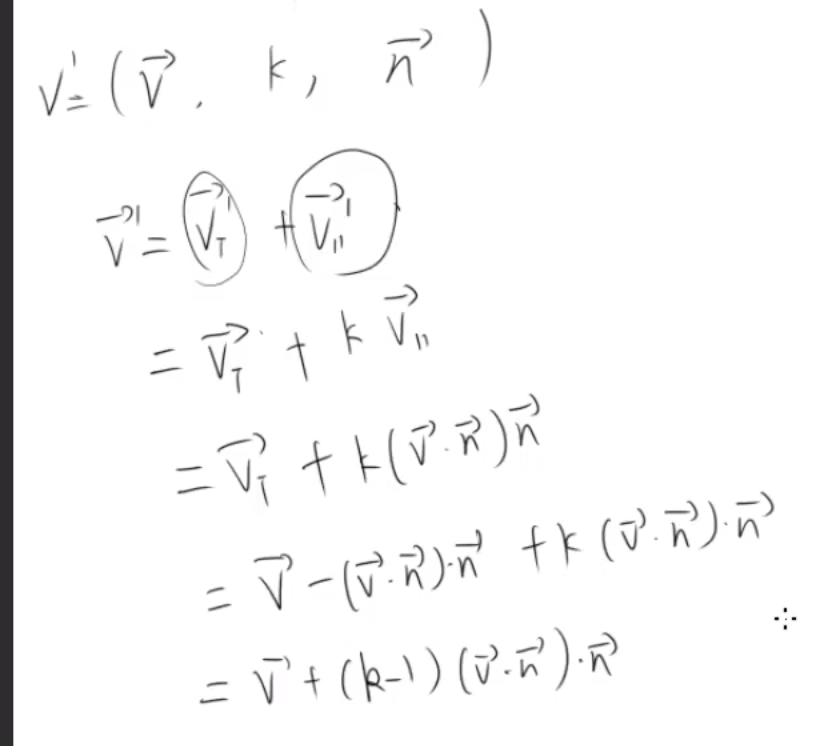
沿轴缩放矩阵
--------------------------
┌ k_x 0 0 ┐
S(k_1, k_2, k_3) = │ 0 k_y 0 │
└ 0 0 k_z ┘
三维绕任意轴旋转矩阵
--------------------------
v' = (v - ( v · n ) n )Cosθ + ( n x v )Sinθ + ( v · n )n
============
叉乘 坐标运算
┌ x_1 ┐ ┌ x_2 ┐ ┌ y_1z_2 - y_2z_1 ┐
│ y_1 │ X │ y_2 │ = │ z_1x_2 - z_2x_1 │
└ z_1 ┘ └ z_2 ┘ └ x_1y_2 - x_2y_1 ┘
============
点乘
┌ x_1 ┐ ┌ x_2 ┐
│ y_1 │ · │ y_2 │ = x_1x_2 + y_1y_2 + z_1z_2
└ z_1 ┘ └ z_2 ┘
============
┌ (n_x)^2(1-Cosθ)+Cosθ ┐
p' = │ n_xn_y(1-Cosθ)+n_zSinθ │
└ n_xn_z(1-Cosθ)-n_ySinθ ┘
┌ n_xn_y(1-Cosθ)-n_zSinθ ┐
q' = │ (n_y)^2(1-Cosθ)+Cosθ │
└ n_yn_z(1-Cosθ)+n_xSinθ ┘
┌ n_xn_z(1-Cosθ)+n_ySinθ ┐
r' = │ n_yn_z(1-Cosθ)-n_xSinθ │
└ (n_z)^2(1-Cosθ)+Cosθ ┘
| p' | ┌ (n_x)^2(1-Cosθ)+Cosθ n_xn_y(1-Cosθ)-n_zSinθ n_xn_z(1-Cosθ)+n_ySinθ ┐
R(n,θ) = | q' | = │ n_xn_y(1-Cosθ)+n_zSinθ (n_y)^2(1-Cosθ)+Cosθ n_yn_z(1-Cosθ)-n_xSinθ │
| r' | └ n_xn_z(1-Cosθ)-n_ySinθ n_yn_z(1-Cosθ)+n_xSinθ (n_z)^2(1-Cosθ)+Cosθ ┘
三维绕任意轴旋转推演
--------------------------
Vector3D v, v';
v·R(n,θ) = v' // v'为v绕n轴旋转θ角度
v' = (v - ( v · n ) n )Cosθ + ( n x v )Sinθ + ( v · n )n
note: ·为点乘, x为叉乘
三维绕轴旋转矩阵
--------------------------
Z轴旋转
┌ Cosθ Sinθ 0 ┐
R(θ) = │ -Sinθ Cosθ 0 │
└ 0 0 1 ┘
X轴旋转
┌ 1 0 0 ┐
R(θ) = │ 0 Cosθ Sinθ │
└ 0 -Sinθ Cosθ ┘
Y轴旋转
┌ Cosθ 0 -Sinθ ┐
R(θ) = │ 0 1 0 │
└ Sinθ 0 Cosθ ┘
左手定则确定方向
| 左手 | 正方向 | 负方向 |
| 从轴的正端点向负端点看 | 顺时针 | 逆时针 |
矩阵乘法特点
--------------------------
矩阵M
单位矩阵 M1
M x M1 = M
=============
矩阵 A, B, C;
(AB)C = A(BC);
=============
矩阵 A, B;
标量 K;
(KA)B = K(AB) = A(KB)
=============
矩阵A, B;
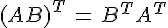
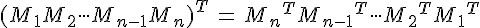
矩阵乘法实际计算
--------------------------
矩阵 A, B;
AB ≠ BA ;
矩阵的乘法
--------------------------
矩阵 A (m x n), B(i x j);
前提: n = i ;
结果: 矩阵C (n x i);
e.g.
┌ a11 a12 ┐ ┌ b11 b12 ┐
A = │ a21 a22 │ B = └ b21 b22 ┘
└ a31 a32 ┘
┌ a11*b11+a12*b21 a11*b21+a12*b22 ┐
A x B = │ a21*b11+a22*b12 a21*b21+a22*b22 │
└ a31*b11+a32*b12 a31*b21+a32*b22 ┘