正交矩阵：

 每行为单位向量

所有行相互垂直

逆矩阵等于矩阵的转置

正交矩阵

--------------------------

定义：MM^(T) = I 

如果 M 是正交矩阵，那么 MM^(T) = I 

结合之前的 M(M^(-1)) = I

那么 M^(T) = M^(-1)

===========

验证一个矩阵是否为正交矩阵，推导

1) 展开 M M^(T) = I

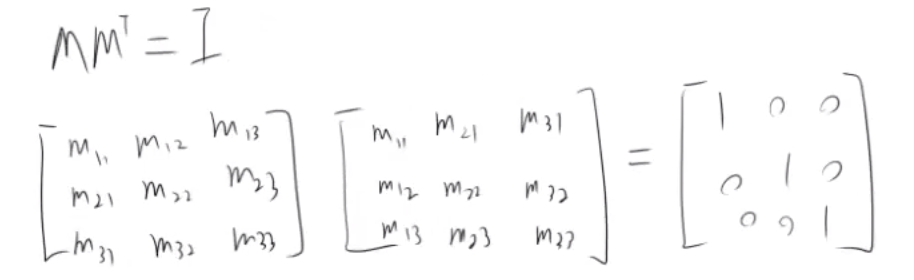
2) 计算 I 的值

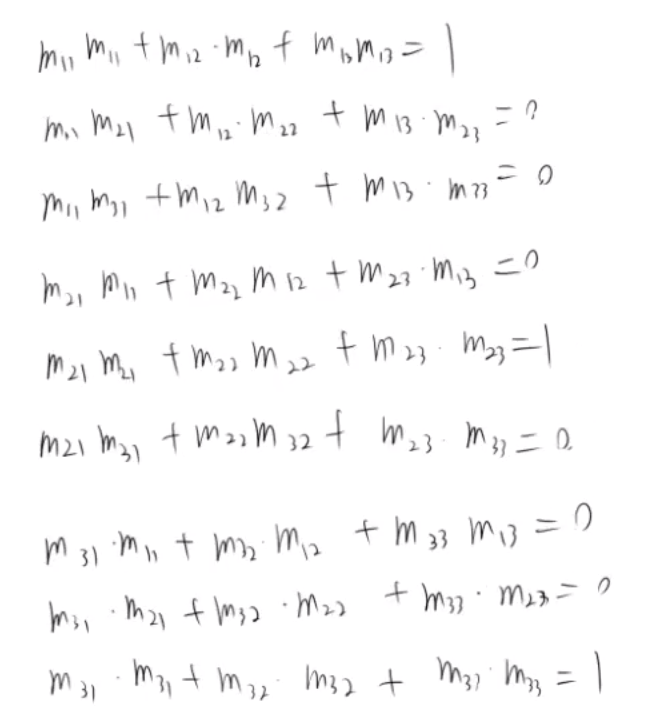
3) 替换M 为三个向量 r_1, r_2, 和 r_3

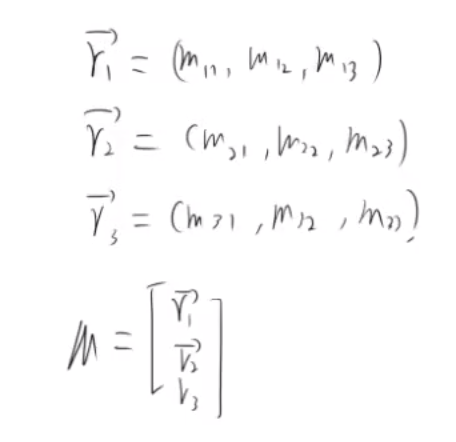
4) 根具 1)、2) 和 3) 可得，再找出重复和特殊的

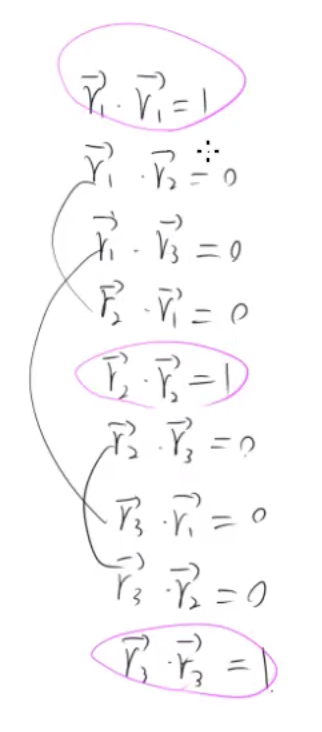
5) 得出结论

      a. 只有当 r_1, r_2 和 r_3 为单位向量时，点积才为1

      b. r_1 ⊥ r_2 ⊥ r_3

      c. 矩阵每行为单位向量

      d. 矩阵所有行互相垂直