续矩阵知识总结-变换总结
--------------------------
行列式性质
1. 行列式与它的转制的值相等 D^T = D
2. 互换行列式两行(列),行列式变号
3. 行列式某一行(列)中所有元素都乘以同一数k,等于用k乘此行列式
4. 如果行列式中如果有两行(列)元素成比例,行列式D = 0
5. 若行列式中某一行(列)的元素都是两数之和,可以把行列式分开写
6. 把行列式某一行(列)的各元素乘以同一数后加到另一行(列)对应元素上,行列不变
==========================================================
代数余子式
A = (-1)^(i+j) M_(ij)
一个n阶行列式,如果其中第i行所有元素除(i,j)元以外都是0,则这个行列式等于 a_(ij) 与它代数余子式的乘积。
D = a_(ij) A_(ij)
行列式等于它的任意一行(列)的各个元素与其对应的代数余子式乘积之和。
D = a_(i1) A_(i1) + a_(i2) A_(i2) + ... + a_(in) A_(in) (i = 1,2, ... , n)
D = a_(1j) A_(1j) + a_(2j) A_(2j) + ... + a_(nj) A_(nj) (j = 1,2, ... , n)
==========================================================
逆矩阵
M(M^(-1)) = M^(-1) M = I
逆矩阵计算公式
M^(-1) = ( adjM )/ ( |M| )
note:adj M 表示 M的伴随矩阵
逆矩阵特性
1) 如果M是非奇异矩阵,则该矩阵的逆的逆等于原矩阵:(M^(-1))^(-1) = M;
2) 单位矩阵的逆是它本身:I^(-1) = I;
3) 矩阵转置的逆等于它的逆的转置:(M^T)^(-1) = ( M^(-1) )^T;
4) 矩阵乘积的逆等于矩阵的逆的相反顺序的乘积:(AB)^(-1) = B^(-1) A^(-1);
5) 根据4) 可拓展到多个矩阵的情况:(M_1 M_2 ... M_n)^(-1) = (M_n)^(-1) (M_(n-1))^(-1) ... (M_1)^(-1);
==========================================================
正交矩阵
M 正交 <=> M M^T = I
M 正交 <=> M^T = M^(-1)
r_1 · r_1 = 1 r_1 · r_2 = 0 r_1 · r_3 = 0
r_2 · r_1 = 0 r_2 · r_2 = 1 r_2 · r_3 = 0
r_3 · r_1 = 0 r_3 · r_2 = 0 r_3 · r_3 = 1
正交矩阵满足条件:
1) 矩阵的每一行都是单位向量
2) 矩阵的所有行相互垂直
正交基:
如果一组向量互相垂直,这组向量就被称作正交基。
标准正交基:
如果一组向量互相垂直并且所有向量都是单位向量,则称为标准正交基。
==========================================================
4 x 4 阶平移矩阵
┌ 1 0 0 0 ┐
[ x y z 1 ] =│ 0 1 0 0 │ = [ x+Δx y+Δy z+Δz 1]
│ 0 1 0 0 │
└ Δx Δy Δz 1 ┘
┌ r_11 r_12 r_13 0 ┐ ┌ 1 0 0 0 ┐ ┌ r_11 r_12 r_13 0 ┐
M = RT =│ r_21 r_22 r_23 0 │ │ 0 1 0 0 │ = │ r_21 r_22 r_23 0 │
│ r_31 r_32 r_33 0 │ │ 0 1 0 0 │ │ r_31 r_32 r_33 0 │
└ 0 0 0 1 ┘ └ Δx Δy Δz 1 ┘ └ Δx Δy Δz 1 ┘
==========================================================
仿射变换

=========================================================
透视投影
┌ x ┐ ┌ -dx/z ┐
p' = │ y │ = │ -dy/z │
└ z ┘ └ -d ┘
┌ 1 0 0 0 ┐
[ x y z 1 ] =│ 0 1 0 0 │ = [ x y z z/d]
│ 0 1 0 1/d│
└ 0 0 0 0 ┘
=========================================================
变换分类
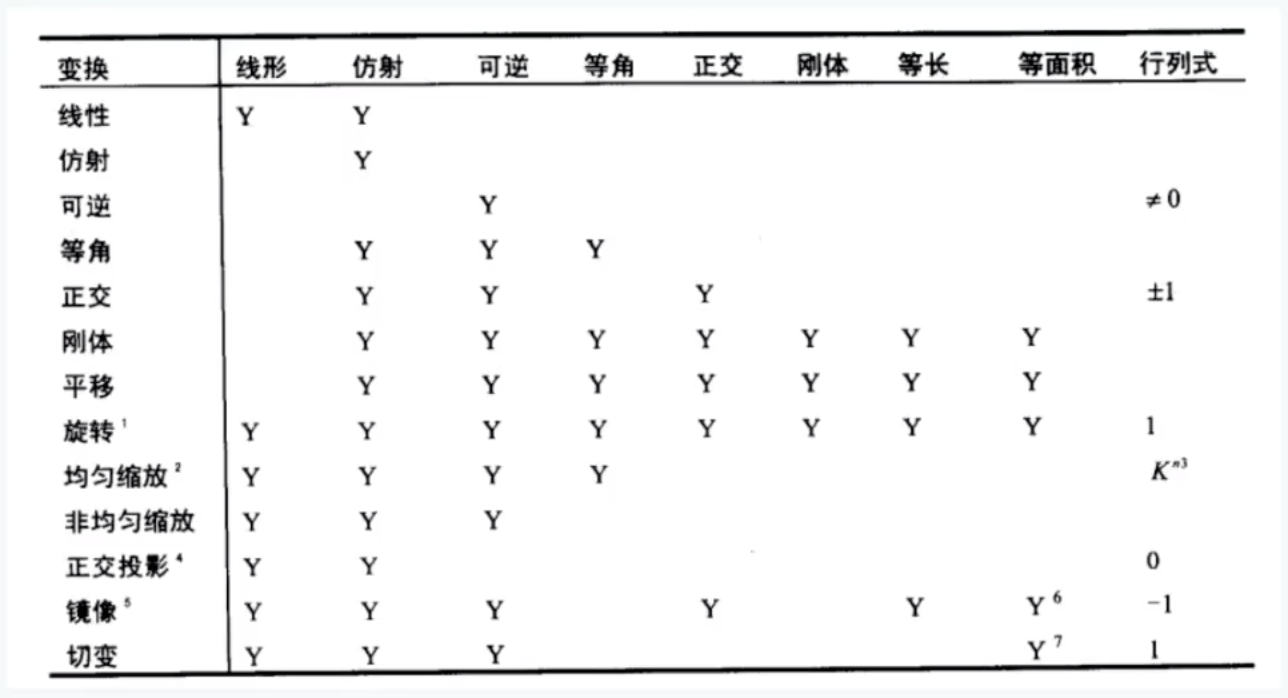
=========================================================
空间变换
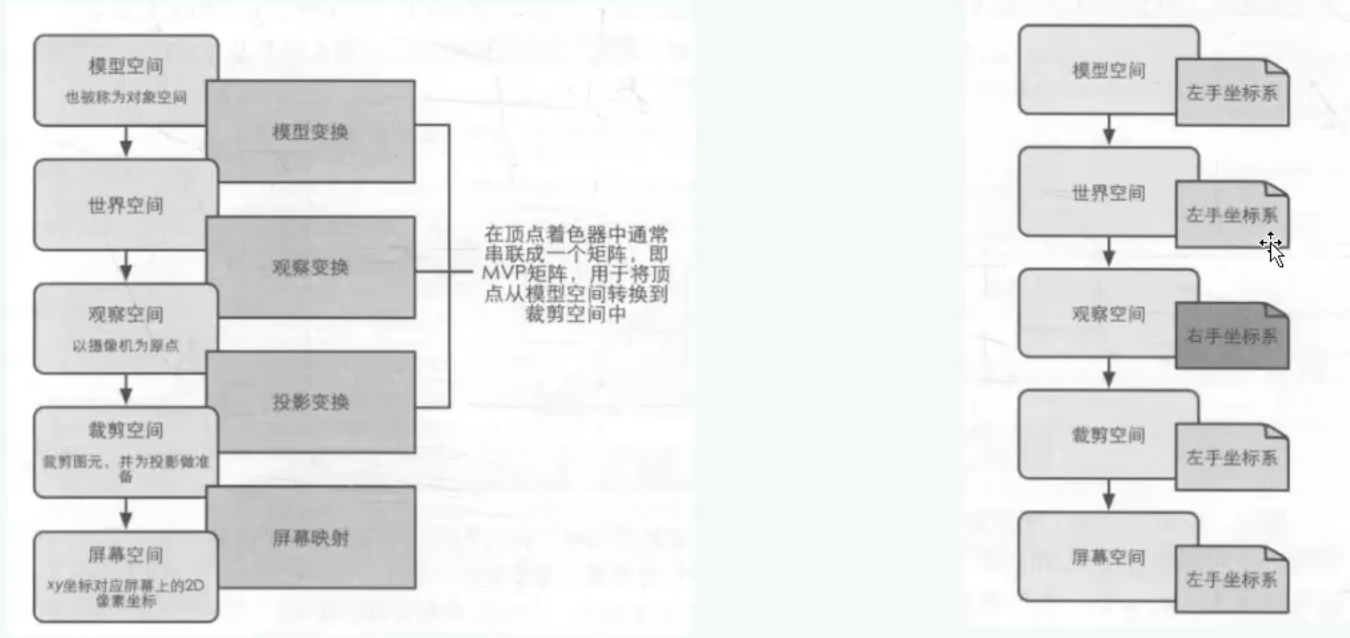
=========================================================
Unity 中透视投影矩阵
┌ n/r 0 0 0 ┐
│ 0 n/t 0 0 │
│ 0 1 -(f+n)/(f-n) (-2fn)/(f-n) │
└ 0 0 -1 0 ┘
存在Zfighting问题:
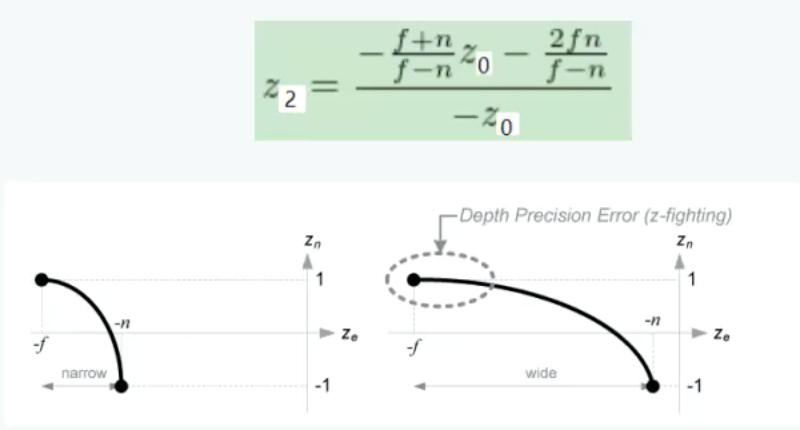
通过上述转换,得到的z值不是线性的,所以为了更精确的表达,所以希望远平面与近平面尽量接近
投影的FOV表达式

=========================================================
Unity 中正交投影矩阵
┌ 1/r 0 0 0 ┐
│ 0 1/t 0 0 │
O = │ 0 1 -2/(f-n) (f+n)/(f-n) │
└ 0 0 -1 0 ┘
改变成Unity的形式






