向量点乘
向量点乘的几何意义
a(向量) * b(向量) > 0
向量夹角 < 90° cos 为 正 [ -90 , 90 ]
a(向量) * b(向量) = 0
向量垂直 cos 为 0 ( -90 , 90 ,270 ,... )
a(向量) * b(向量) < 0
向量夹角 > 90° cos 为 负 [ -90 , -270 ]
向量的点乘 有 2 个公式
( 这2个公式求得的最后结果都是一样的,一个标量 )
公式1:
OA(向量) * OB(向量) = ( x1 * x2 ) + ( y1 * y2 )
公式2:
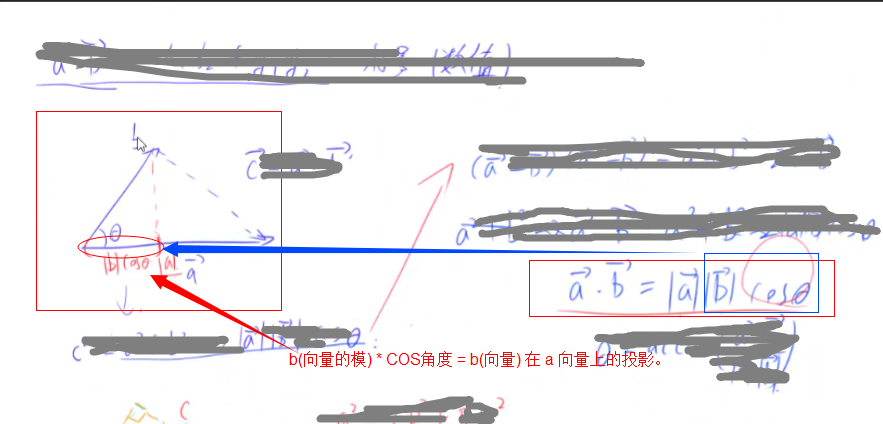
OA(向量) * OB(向量) = OA(向量的模) * OB(向量的模) * COS(向量夹角)
(1、灵活运用这2个公式可以求的俩个向量的点乘
2、也可以求的俩个向量的夹角
3、一个向量在另一个向量上的投影。)
俩个向量之间的点乘相当于,A 向量在 B 向量上的投影 * B 向量的模长