每次脱节的时候，相机进行旋转

创建bool标识，在火箭脱落到最后一节，摄像机停止跟随

创建相机脚本，定义跟随对象，偏移量

更新位置的代码，写在LateUpdate（）中，否则会有抖动的效果

每次跟新目标点方法

tween杀死动画的api  .Kill

火箭头变短方法，主要通过改变Z轴

重新创建Transform[]，

当前索引必须小于数组Length-1，否则return;

当索引等于数组长度，代表最后一节已经脱落

火箭脱落一节，速度对应增加1

创建火箭部分脱落方法，Update中鼠标左键按下调用

思路：脱离父对象，作为单独一个部分，不随着火箭整体移动

定义transform[]类型的数组

 Time.time  运行程序即开始ji'shi

创建玩家数据管理类，UI管理类，音频管理类

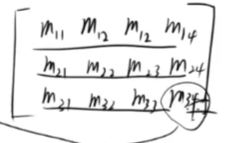
矩阵的简单介绍

矩阵分 行 和 列

例如：

3 X 4 阶矩阵

3 是 行

4 是 列

不错！

    // Stretch a mesh at an arbitrary angle around the X axis.

    // Angle and amount of stretching.

    public float rotAngle;

    public float stretch;

    MeshFilter mf;

    Vector3[] origVerts;

    Vector3[] newVerts;

    void Start()

    {

        // Get the Mesh Filter component, save its original vertices

        // and make a new vertex array for processing.

        mf = GetComponent< MeshFilter > ();

        origVerts = mf.mesh.vertices;

        newVerts = new Vector3[origVerts.Length];

    }

    void Update()

    {

        // Create a rotation matrix from a Quaternion.

        Quaternion rot = Quaternion.Euler(rotAngle, 0, 0);

        Matrix4x4 m = Matrix4x4.TRS(Vector3.zero, rot, Vector3.one);

        // Get the inverse of the matrix (ie, to undo the rotation).

        Matrix4x4 inv = m.inverse;

        // For each vertex...

        for (var i = 0; i < origVerts.Length; i++)

        {

            // Rotate the vertex and scale it along its new Y axis.

            var pt = m.MultiplyPoint3x4(origVerts[i]);

            pt.y *= stretch;

            // Return the vertex to its original rotation (but with the

            // scaling still applied).

            newVerts[i] = inv.MultiplyPoint3x4(pt);

        }

        // Copy the transformed vertices back to the mesh.

        mf.mesh.vertices = newVerts;

    }

沿着x轴反向旋转，然后y方向拉伸，然后再旋转回来

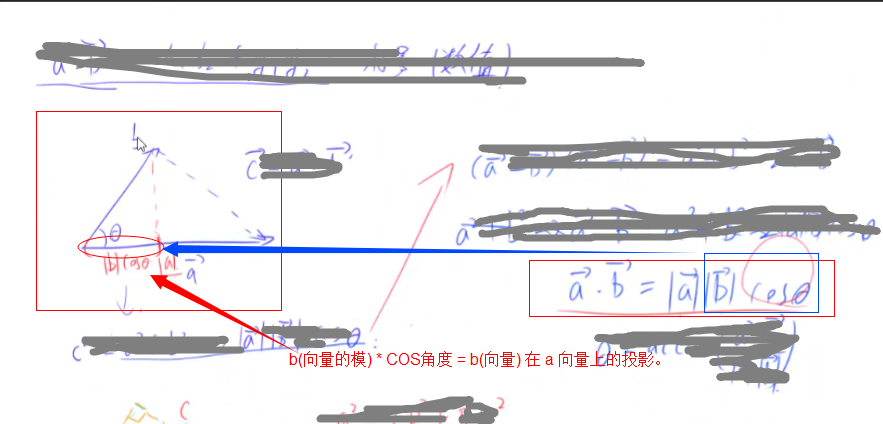
向量点乘

向量点乘的几何意义

 a(向量） * b(向量) > 0  

向量夹角 < 90°  cos 为 正  [ -90 , 90 ]

a(向量） * b(向量) = 0 

 向量垂直  cos 为 0  （ -90 , 90 ，270 ，... )

a(向量） * b(向量) < 0  

向量夹角 > 90°   cos 为 负  [ -90 , -270 ]

向量的点乘 有 2 个公式

（ 这2个公式求得的最后结果都是一样的，一个标量 ）

公式1：

OA(向量) * OB(向量) = ( x1 * x2 ) + ( y1 * y2 )

公式2：

OA(向量) * OB(向量) = OA(向量的模) * OB(向量的模)  * COS（向量夹角）

（1、灵活运用这2个公式可以求的俩个向量的点乘

2、也可以求的俩个向量的夹角 

3、一个向量在另一个向量上的投影。）

俩个向量之间的点乘相当于，A 向量在 B 向量上的投影 * B 向量的模长

三维向量叉乘

I a(向量) x b(向量) I = I a(向量) I I b(向量) I sin角度

叉乘得到的最终向量的方面，按照所遵循的左手和右手定则 而不同。

叉乘的意义：

判断三角面的朝向。

叉乘的值

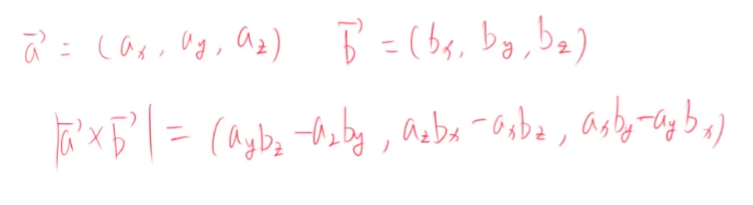
#### 叉积的应用

* 得到一个平面的法向量

* 判断旋转方向：axb旋转方向就是从a到b，顺时针和逆时针取决于观察方向，走到对侧观察，顺逆性就刚好反过来了。

** 用左手定则，假设知道了axb（中指），和a（大拇指），我们大致可以判断b的方向，知道axb（大拇指）和b（食指）也是一样。在该系中，axb，a到b永远是顺时针。 +

就是说，站在大拇指和食指形成的平面，头朝向axb观察，是顺时针，顺时针就是角度变大的旋转方向。

** 0 共线（可能同向，或反向）

### unity中的点和向量

vector2 vector3 分别用来表示二维 或 三维 的点或向量。

* transform.position transform所在对象在世界坐标系中的点的位置

* transform.forwoard 等相关值，是transform所在对象z正向在世界坐标系的单位向量

* 在unity中，用vector3来表示对象的位置

* 在unity中，*用vector3来表示物体移动的长度和方向*。

** update函数相当于差分，每帧移动ds距离

** 设匀速运动s=vt,则ds=v*dt，从t到t+1秒积分得：s=v，也就是说，累积一秒的若干帧更新，刚好走过了速度标定的距离，因此我们也把向量当作速度来用

*** update函数中的移动距离计算为：ds=time.deltatime*移动矢量，其中移动矢量是一秒物体移动的距离，也就是速度

* 在unity中，可以通过两个对象transform.position值相减得到的矢量的模，得到两个对象的距离

[source,csharp]

----

private Vector3 movingvect;

private bool movingSetted=false;

private float movingtime=3;

//set in inspector panel

public  Transform target;

// Update is called once per frame

void Update()

{

    //第一次，求移动矢量，也就是距离

    if (movingSetted==false){

        movingSetted=true;

        movingvect=target.position-transform.position;

    }

    //距离足够小停止运动

    var distanceVector=target.position-transform.position;

    //模平方获得较好运行性能

    if(Vector3.SqrMagnitude(distanceVector)>=0.1f)

    transform.Translate(movingvect/movingtime*Time.deltaTime,Space.World);

}

----

    void Update()

    {

        //每秒移动两秒抵达屏幕边界时停止

        var vpp = Camera.main.WorldToViewportPoint(transform.position);

        if (vpp.x > 0 && vpp.y > 0 && vpp.x < 1 && vpp.y < 1)

            transform.Translate(Time.deltaTime * Vector3.right * 2, Space.World);

    }

### 屏幕坐标与视口坐标转换

#### Camera.ScreenToViewportPoint

public Vector3 ScreenToViewportPoint(Vector3 position);

Transforms position from screen space into viewport space.

Screenspace is defined in pixels. The bottom-left of the screen is (0,0); the right-top is (pixelWidth,pixelHeight). The z position is in world units from the camera.

#### Camera.ViewportToScreenPoint

public Vector3 ViewportToScreenPoint(Vector3 position);

Transforms position from viewport space into screen space.

Viewport space is normalized and relative to the camera. The bottom-left of the camera is (0,0); the top-right is (1,1). The z position is in world units from the camera.

//下列两条语句等价

transform.Translate(Time.deltaTime*transform.up,Space.World);

transform.Translate(Time.deltaTime*Vector3.up);

## 坐标系关联与相互转换

### Transform.Translate

`public void Translate(Vector3 translation, Space relativeTo = Space.Self);`

将transform，相对于space坐标系，移动translation的距离

* 移动谁：移动transform所在对象

* 相对于哪个坐标系移动：相对于space移动

* 移动多少：移动translation

* space枚举取值有哪些：space.world,space.self(默认值)

## Transform.TransformPoint

`public Vector3 TransformPoint(Vector3 position);`

将本transform空间中的点position，转换到世界坐标系。

## Transform.InverseTransformPoint

`public Vector3 InverseTransformPoint(Vector3 position);`

将世界坐标系中的点position，转换到本transform的局部坐标系