学数学头大啊,不想学啊,但是又不能不学,TAT
1/r 0 0 0
0 1/t 0 0
0 0 -2/fn (-f+n)/(f-n)
0 0 0 0
学数学头大啊,不想学啊,但是又不能不学,TAT
1/r 0 0 0
0 1/t 0 0
0 0 -2/fn (-f+n)/(f-n)
0 0 0 0
Unity中透视投影矩阵
--------------------------

平面投影
--------------------------
结合初中知识 小孔成像 得出结论
当物体在原点前,投影平面在原点后,距离为d
┌ x ┐ ┌ x ┐ ┌ -dx/z ┐
p = │ y │ = > p' = │ y │ = │ -dy/z │
└ z ┘ └ z ┘ └ -d ┘
当投影平面也在原点前,距离为d时
┌ x ┐ ┌ -dx/z ┐
p' = │ y │ = │ -dy/z │
└ z ┘ └ -d ┘
一般仿射变换
--------------------------
当做 绕不通过原点的轴旋转 或 沿不穿过原点的平面缩放 等类似的题目时
1) P向量使用平移矩阵T移到原点
2) P向量使用矩阵R进行线性变换
3) P向量使用矩阵T的逆矩阵T^(-1)移到之前位置
P T R T^(-1)
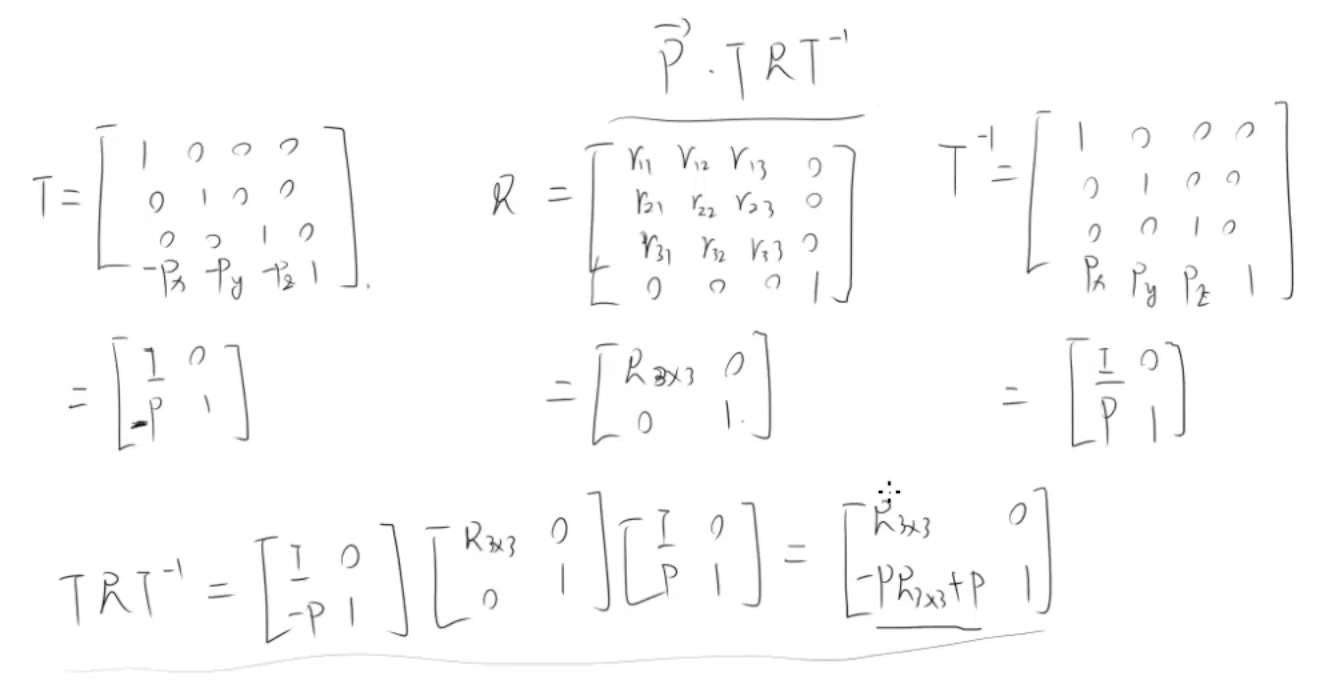
平移只影响到了4x4阶矩阵的最后一行的元素,而对它的其他的旋转矩阵或者线性矩阵没有任何影响
==============
判断矩阵是否可逆: |M| ≠ 0
奇异矩阵/不可逆矩阵:一个不可逆矩阵 |M| = 0
逆矩阵计算公式
--------------------------
e.g.
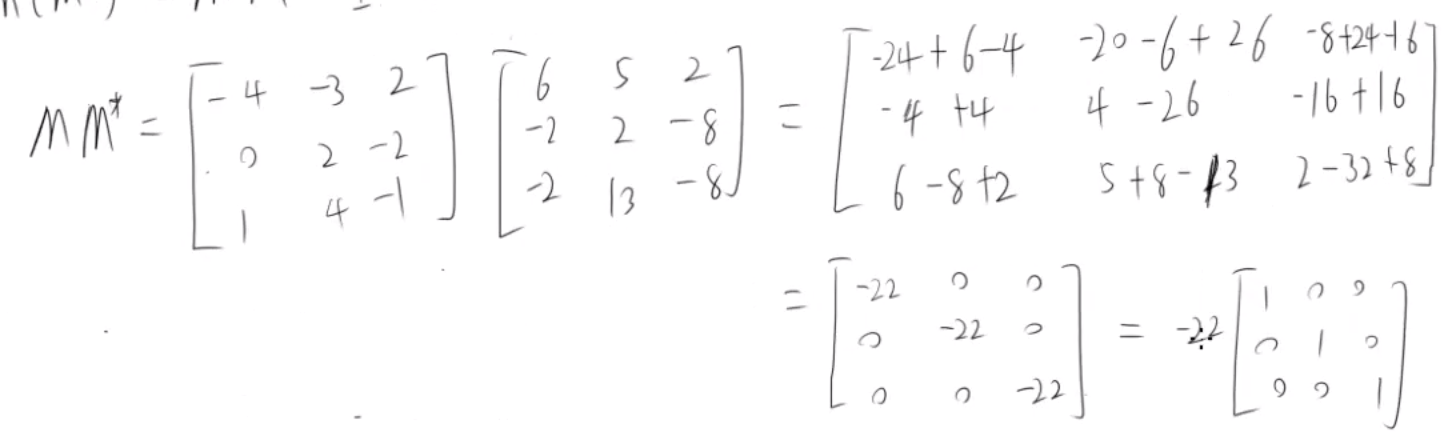
===========
结合 |M| 来看
MM* = |M| I = M*M
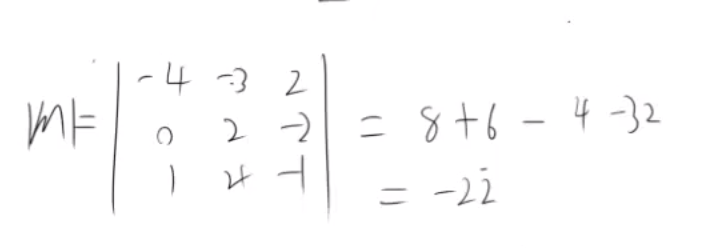
note:M* 为 M 的伴随矩阵
============
M M* = |M| I
M ( M* / |M| ) = I
M M^(-1) = I
M^(-1) = M* / |M|
变换分类
--------------------------
线性变换
F(a + b) = F(a) + F(b)
F(ka) = kF(a)
============
F(a) = am // m为任意方阵
F(a + b) = (a + b) m
= am + bm
= F(a) + F(b)
F( ka ) = (ka) M
= k (am)
= k F(a)
============
如果 F(0) = a, 且 a ≠ 0, 那么 F不可能是线性变换
F(k0) = a F(k0) ≠ kF(0)
线性变换不会出现平移,因为原点位置上不会变化
============
反射变换
反射变换是指线性变换后接着平移
Vector V
Matrix M
V' = VM + b //反射变换
============
可逆变换
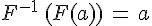
V' = VM V = V'M^(-1)
============
等角变换
变换前后夹角大小方向不变
============
正交变换
============
刚体变换
============

旋转矩阵与平移矩阵结合
--------------------------
1) 已知旋转矩阵 R 和平移矩阵 T
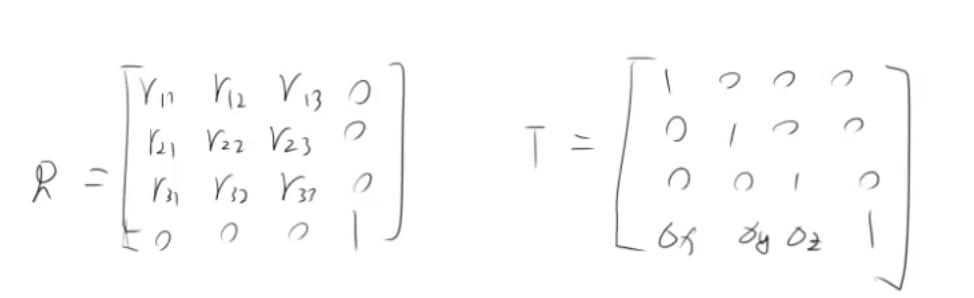
2) 根据公式,可得矩阵
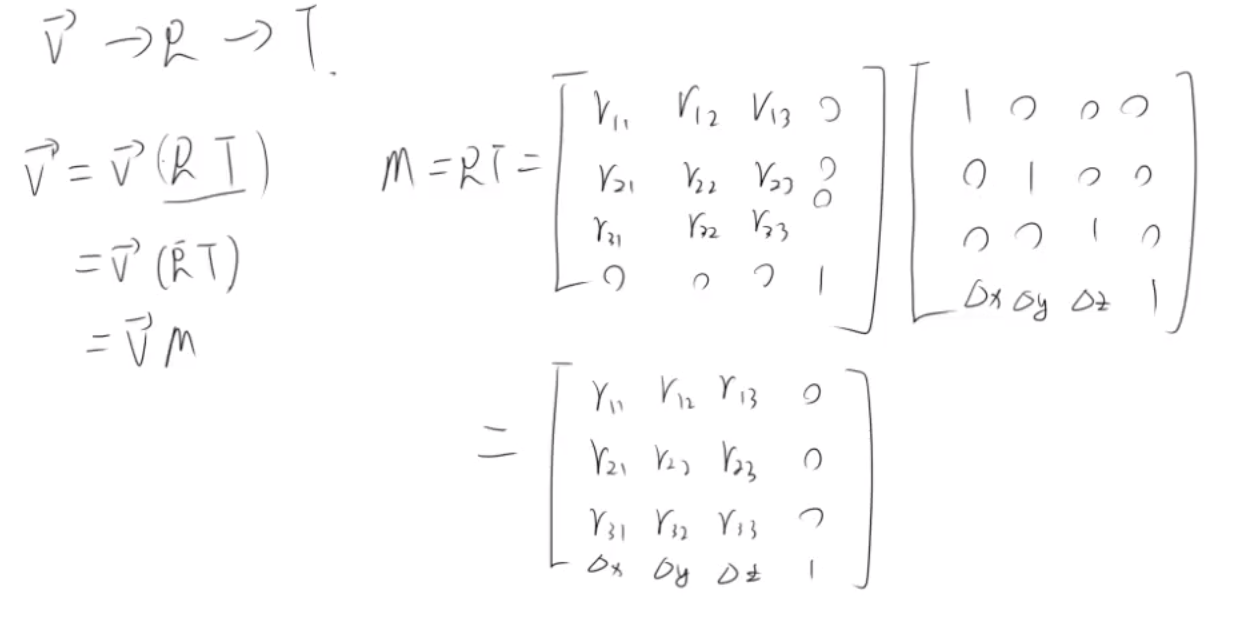
3) 如果把 [Δx, Δy, Δz] = t, 那么可得

平移矩阵
--------------------------
2D齐次坐标 (x, y, w) 3x3阶
3D齐次坐标 (x, y, z, w) 4x4阶
==================
4x4 阶平移矩阵
1) 一般三维坐标
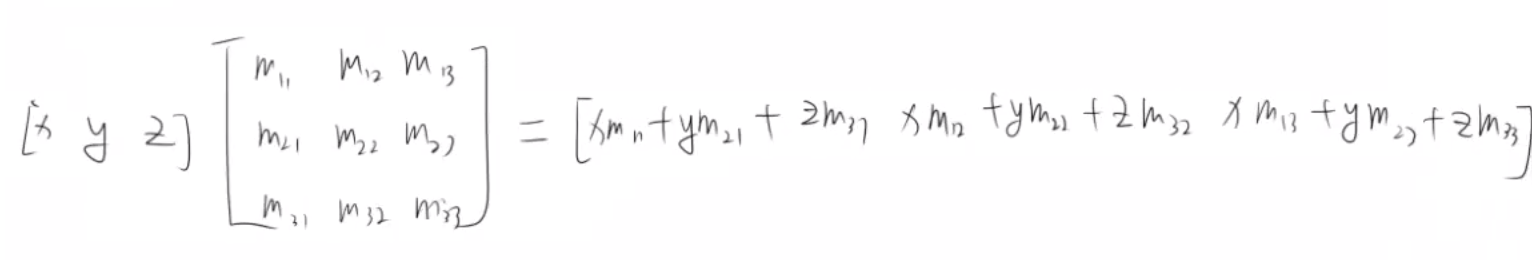
2) 加入 w 变为齐次坐标
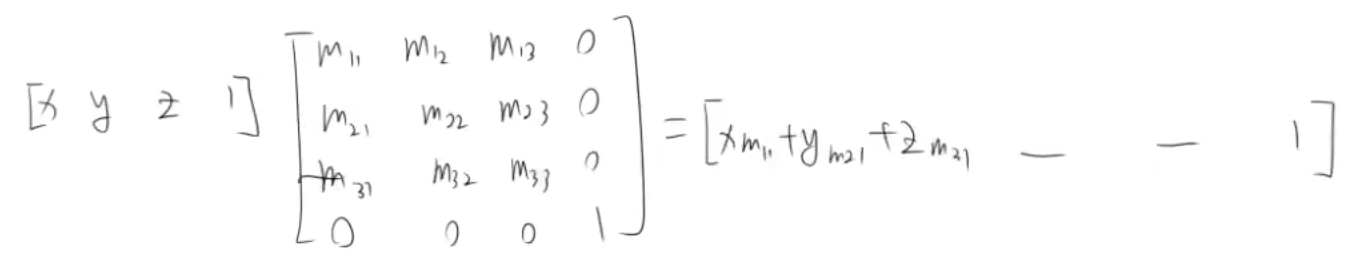
3) 转换矩阵为单位矩阵并加入 Δx, Δy和Δz来实现平移
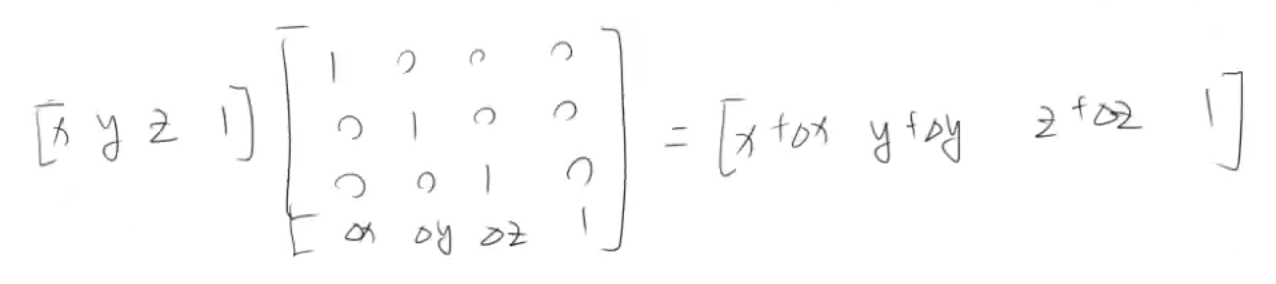
齐次空间
--------------------------
对于一个2D的点 ( x, y ),在齐次空间中表示为 (x, y, w),那么2D点的真实表示发生为 2D(x/w, y/w )
在2D中 如果w = 0, 那么表示无限远的一个点
对于一个3D的点 ( x, y, z ),在齐次空间中表示为 (x, y, z, w),那么3D点的真实表示发生为 3D(x/w, y/w, z/w)
在3D中 如果w = 0, 那么表示无限远的一个点
======
目的:为了之后做平移点变换
正交基与标准正交基
--------------------------
一组正交基:基矢量直接互相垂直
标准正交基:给个基矢量长度为1
正交矩阵是一组标准正交基
如果使用一组正交基构建矩阵,不一定是正交矩阵
===========
施密特正交化
施密特正交化(Schmidt orthogonalization)是求欧氏空间正交基的一种方法。从欧氏空间任意线性无关的向量组α1,α2,……,αm出发,求得正交向量组β1,β2,……,βm,使由α1,α2,……,αm与向量组β1,β2,……,βm等价,再将正交向量组中每个向量经过单位化,就得到一个标准正交向量组,这种方法称为施密特正交化。
Reference:
百度百科, 2018, 施密特正交化, Link: https://baike.baidu.com/item/%E6%96%BD%E5%AF%86%E7%89%B9%E6%AD%A3%E4%BA%A4%E5%8C%96/756386?fr=aladdin [Accessed Date: 2018/04/12]
正交矩阵
--------------------------
定义:MM^(T) = I
如果 M 是正交矩阵,那么 MM^(T) = I
结合之前的 M(M^(-1)) = I
那么 M^(T) = M^(-1)
===========
验证一个矩阵是否为正交矩阵,推导
1) 展开 M M^(T) = I
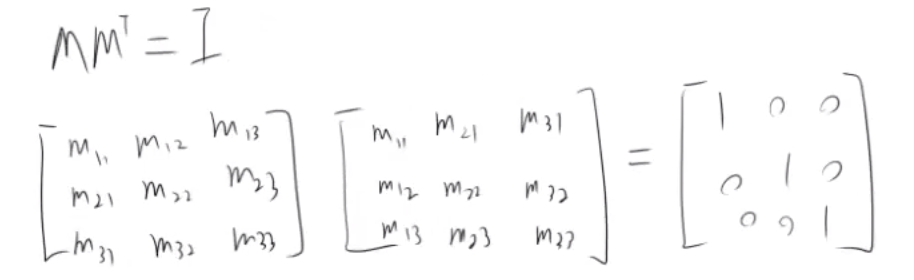
2) 计算 I 的值
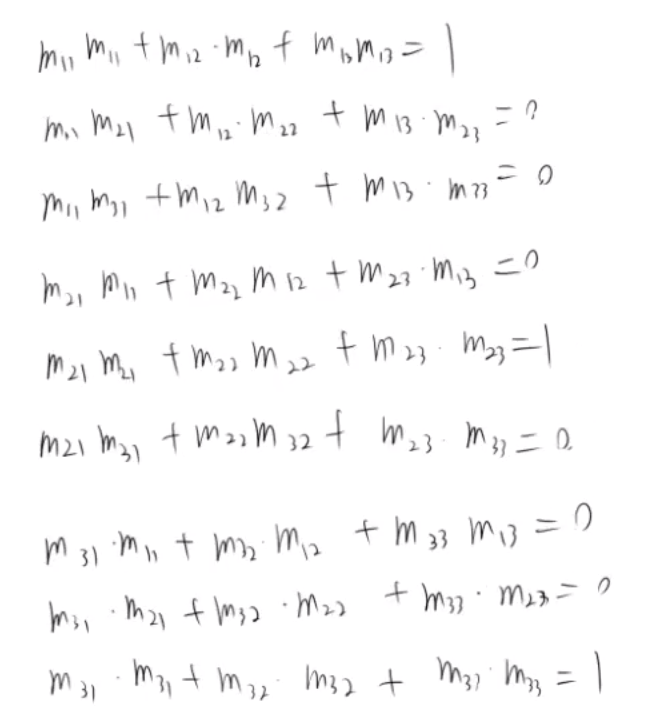
3) 替换M 为三个向量 r_1, r_2, 和 r_3
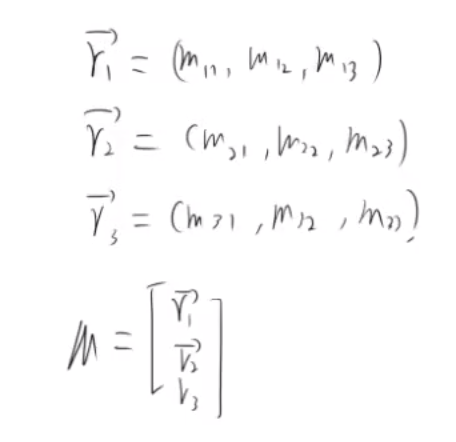
4) 根具 1)、2) 和 3) 可得,再找出重复和特殊的
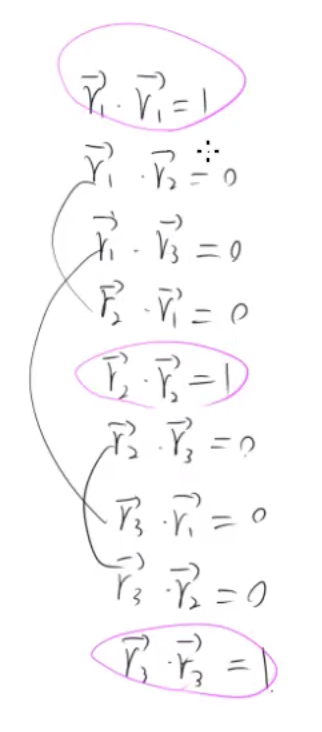
5) 得出结论
a. 只有当 r_1, r_2 和 r_3 为单位向量时,点积才为1
b. r_1 ⊥ r_2 ⊥ r_3
c. 矩阵每行为单位向量
d. 矩阵所有行互相垂直

继承的一个作用:代码复用和结构复用
方法:算法逻辑代码复用
泛型:结构进行复用
伴随矩阵
--------------------------
行列式性质复习
1. 行列式与它的转置行列式相等
2. 互换行列式两行(列),行列式变号
3. 行列式的某一行)(列)中所有元素都乘以同一数k,等于用数k乘此行列式
4. 行列式中如果又两行(列)成比例,则此行列式等于零
5. 若行列式都某一行(列)的元素都是两数之和,那么可以拆分成两个行列式
6.把行列式的某一行(列)的个元素乘以同一数然后加到另一行(列)对应的元素上,行列式不变
==============
几何解释
2D中,行列式等于以基向量为两边的平行四边形的有符号面积
3D中,行列式等于以变换后的基向量为三边的平行六边形的有符号体积
==============
伴随矩阵:矩阵M每一个元素的代数余子式所围成的矩阵的转置
M = A^T
e.g.
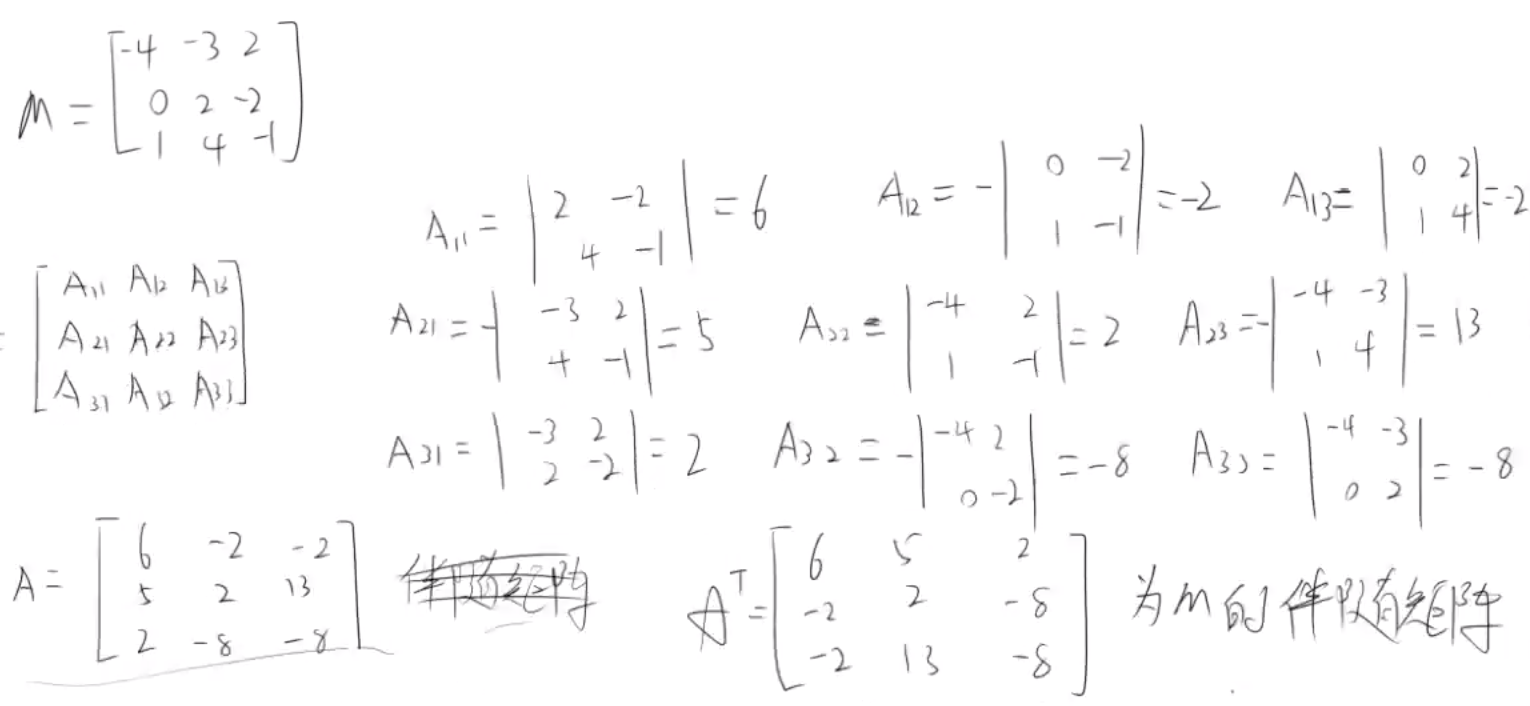
伴随矩阵和矩阵的逆有关系
M (M^(-1)) = M^(-1) M = I
行列式按行按列展开法则
--------------------------
行列式等于它的任意行(列)的各元素与其对应的代数余子式乘积之和;
(更具性质:若行列式中某一行(列)的元素都是两数之和,可以把行列式分开写)
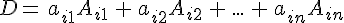
代数余子式性质
--------------------------
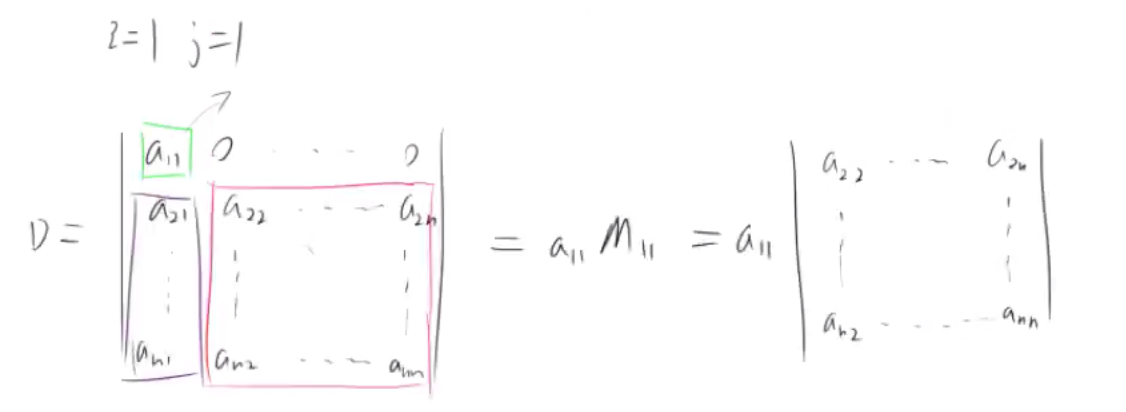
证明:D = a_(ij)A_(ij)
如果a_(ij) 在第一行第一列
===================
如果a_(ij) 不在第一行第一列
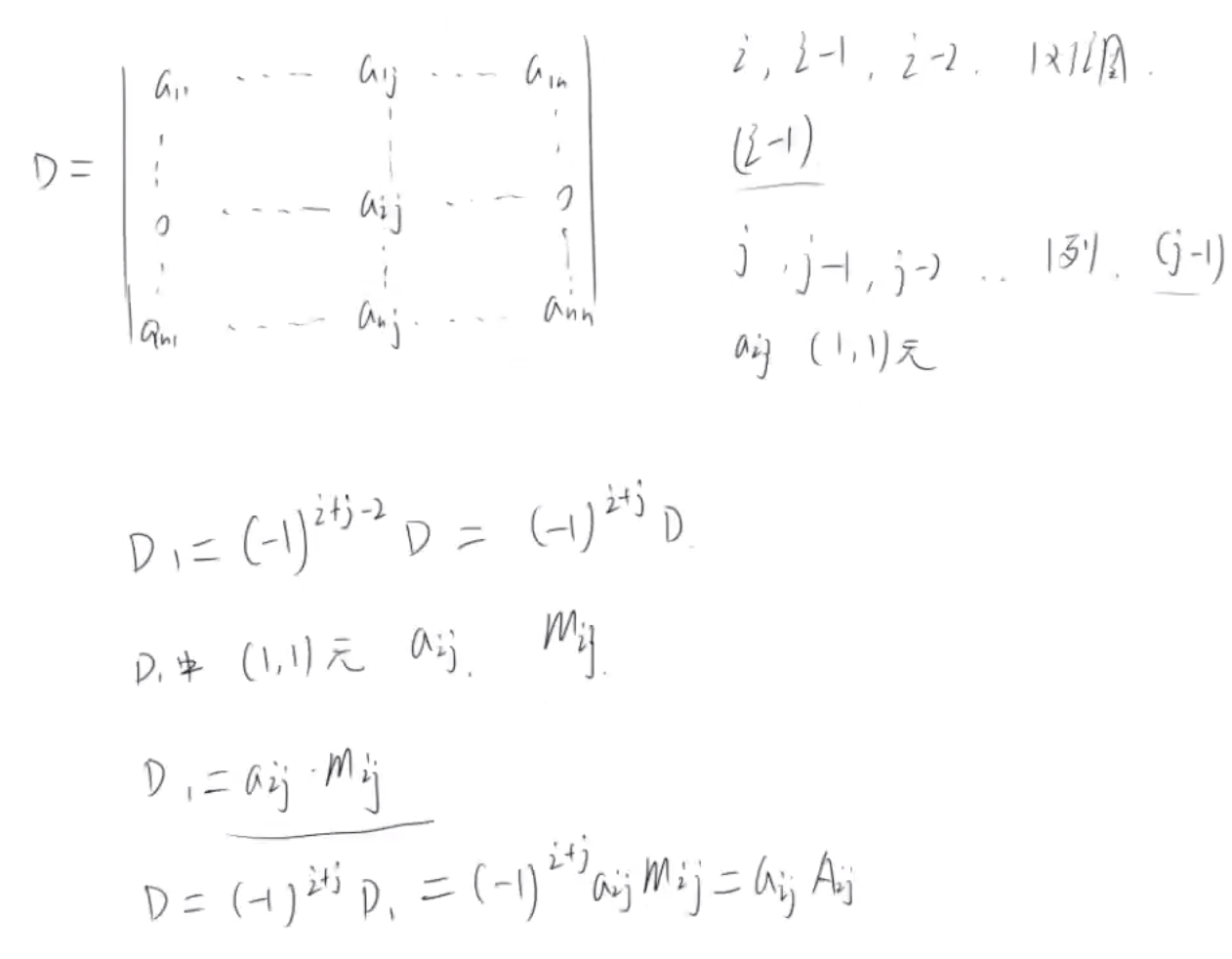
什么。0时泛型:泛型就是可以下先不定义等使用的时候再定义
学到的性知识点
泛型是结构的复用
方法是逻辑的复用
params 可变参数
会造成xiao
行列式证明三角行列式性质
--------------------------
如果已知

那么 D = D_1D_2
==================
一个n阶行列式,如果其中第i行所有元素除(i,j)元 a_(ij) 外都为0,那么这个行列式就等于:
D = a_(ij)A_(ij)
三阶行列式
--------------------------
| m_11 m_12 m_13 |
M = | m_21 m_22 m_23 |
| m_31 m_32 m_33 |
| M | = m_11m_22m33 +m_12m_23m_32 + m_13m_21m_32 - m_13m_22m_31 - m_32m_23m_11 - m_21m_12m_33 ;
==============
三维叉乘
Vector3D a,b;
i = (1,0,0)
j = (0,1,0)
k = (0,0,1)
| i j k |
a x b = | a.x a.y a.z | = (a.y b.z - b.y a.z)i - (a.x b.z - b.x a.z)j + (a.x b.y - b.x a.y)k ;
| b.x b.y b.z |
a x b = (a.y b.z - b.y a.z)i - (a.x b.z - b.x a.z)j + (a.x b.y - b.x a.y)k ;
二阶行列式
--------------------------
| m_11 m_12 |
M = | m_21 m_22 |
| M | = m_11m_22 - m_12m_21
=====================
extra note:
行列式与矩阵的区别与联系
1、行列式的本质是线性变换的放大率,而矩阵的本质就是个数表。
2、行列式行数=列数,矩阵不一定(行数列数都等于n的叫n阶方阵),二者的表示方式亦有区别。
3、行列式与矩阵的运算明显不同
1) 相等:只有两个同型的矩阵才有可能相等,并且要求对应元素都相等;而两个行列式相等不要求其对应元素都相等,甚至阶数还可以不一样,只要两个行列式作为两个数的值是相等即可。
2) 加(减)法:两个矩阵相加(减)是将其对应元素相加(减),因此只有同型的矩阵才可以相加(减);而两行列式作为两个数总是可以相加(减)的。
3) 数乘运算:一个数乘以矩阵是指该数乘以矩阵的每一个元素;而数乘行列式,只能用此数乘行列式的某一行或列,提取公因数也是如此。
4) 乘法:矩阵的乘法不满足交换律,所以,一般地, AB≠BA。但是,如果 A与 B 都是 n 阶方阵,则有 |AB|=|A| |B|=|B| |A|=|BA|。
Reference:
百度知道, 2018, 行列式与矩阵的区别与联系, Link: https://zhidao.baidu.com/question/97241681.html [Accessed Date: 2018/04/12]